This is the sixth post in my series about named entity recognition. If you haven’t seen the last five, have a look now. The last time we used character embeddings and a LSTM to model the sequence structure of our sentences and predict the named entities. This time I’m going to show you some cutting edge stuff. We will use a residual LSTM network together with ELMo embeddings [1], developed at Allen NLP. You will learn how to wrap a tensorflow hub pretrained model to work with keras. The resulting model with give you state-of-the-art performance on the named entity recognition task.
What are ELMo embeddings?
ELMo embeddings are embeddings from a language model trained on the 1 Billion Word Benchmark and the pretrained version is available on tensorflow hub. Unlike most widely used word embeddings, ELMo word representations are functions of the entire input sentence. They are computed on top of two-layer bidirectional language model with character convolutions, as a linear function of the internal network states. Concretely, ELMos use a pre-trained, multi-layer, bi-directional, LSTM-based language model and extract the hidden state of each layer for the input sequence of words. Then, they compute a weighted sum of those hidden states to obtain an embedding for each word. The weight of each hidden state is task-dependent and is learned. ELMo improves the performance of models across a wide range of tasks, spanning from question answering and sentiment analysis to named entity recognition. This setup allows us to do semi-supervised learning, where the biLM is pre-trained at a large scale and easily incorporated into a wide range of existing neural NLP architectures.
I suggest having a look at the great paper “Deep contextualized word representations”.
Data preperation
Let’s start by loading and preparing the data. If you are familiar with the last post of this series, you can skip this part and jump directly to the model setup. If you want to run the tutorial yourself, you can find the dataset here.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use("ggplot")
data = pd.read_csv("ner_dataset.csv", encoding="latin1")
data = data.fillna(method="ffill")
data.tail(10)
| Sentence # | Word | POS | Tag | |
|---|---|---|---|---|
| 1048565 | Sentence: 47958 | impact | NN | O |
| 1048566 | Sentence: 47958 | . | . | O |
| 1048567 | Sentence: 47959 | Indian | JJ | B-gpe |
| 1048568 | Sentence: 47959 | forces | NNS | O |
| 1048569 | Sentence: 47959 | said | VBD | O |
| 1048570 | Sentence: 47959 | they | PRP | O |
| 1048571 | Sentence: 47959 | responded | VBD | O |
| 1048572 | Sentence: 47959 | to | TO | O |
| 1048573 | Sentence: 47959 | the | DT | O |
| 1048574 | Sentence: 47959 | attack | NN | O |
words = list(set(data["Word"].values))
words.append("ENDPAD")
n_words = len(words); n_words
35179
tags = list(set(data["Tag"].values))
n_tags = len(tags); n_tags
17
So we have 47959 sentences containing 35178 different words with 17 different tags. We use the SentenceGetter class from last post to retrieve sentences with their labels.
class SentenceGetter(object):
def __init__(self, data):
self.n_sent = 1
self.data = data
self.empty = False
agg_func = lambda s: [(w, p, t) for w, p, t in zip(s["Word"].values.tolist(),
s["POS"].values.tolist(),
s["Tag"].values.tolist())]
self.grouped = self.data.groupby("Sentence #").apply(agg_func)
self.sentences = [s for s in self.grouped]
def get_next(self):
try:
s = self.grouped["Sentence: {}".format(self.n_sent)]
self.n_sent += 1
return s
except:
return None
getter = SentenceGetter(data)
sent = getter.get_next()
This is how a sentence looks now.
print(sent)
[('Thousands', 'NNS', 'O'), ('of', 'IN', 'O'), ('demonstrators', 'NNS', 'O'), ('have', 'VBP', 'O'), ('marched', 'VBN', 'O'), ('through', 'IN', 'O'), ('London', 'NNP', 'B-geo'), ('to', 'TO', 'O'), ('protest', 'VB', 'O'), ('the', 'DT', 'O'), ('war', 'NN', 'O'), ('in', 'IN', 'O'), ('Iraq', 'NNP', 'B-geo'), ('and', 'CC', 'O'), ('demand', 'VB', 'O'), ('the', 'DT', 'O'), ('withdrawal', 'NN', 'O'), ('of', 'IN', 'O'), ('British', 'JJ', 'B-gpe'), ('troops', 'NNS', 'O'), ('from', 'IN', 'O'), ('that', 'DT', 'O'), ('country', 'NN', 'O'), ('.', '.', 'O')]
Okay, that looks as expected, now get all sentences.
sentences = getter.sentences
For the use of neural nets (at least with keras, there is no theoretical reason) we need to use equal-length input sequences. So we are going to pad our sentences to a length of 50. But first we need a dictionary of tags to map our labels to numbers.
max_len = 50
tag2idx = {t: i for i, t in enumerate(tags)}
tag2idx["B-geo"]
14
To apply the EMLo embedding from tensorflow hub, we have to use strings as input. So we take the tokenized sentences and pad them to the desired length.
X = [[w[0] for w in s] for s in sentences]
new_X = []
for seq in X:
new_seq = []
for i in range(max_len):
try:
new_seq.append(seq[i])
except:
new_seq.append("__PAD__")
new_X.append(new_seq)
X = new_X
This is how a input sample looks like now.
print(X[1])
['Iranian', 'officials', 'say', 'they', 'expect', 'to', 'get', 'access', 'to', 'sealed', 'sensitive', 'parts', 'of', 'the', 'plant', 'Wednesday', ',', 'after', 'an', 'IAEA', 'surveillance', 'system', 'begins', 'functioning', '.', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__', '__PAD__']
And we need to do the same for our tag sequence, but map the string to an integer.
y = [[tag2idx[w[2]] for w in s] for s in sentences]
from keras.preprocessing.sequence import pad_sequences
y = pad_sequences(maxlen=max_len, sequences=y, padding="post", value=tag2idx["O"])
Using TensorFlow backend.
y[1]
array([ 0, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 11, 15,
15, 15, 4, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15,
15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15],
dtype=int32)
We split in train and test set.
from sklearn.model_selection import train_test_split
X_tr, X_te, y_tr, y_te = train_test_split(X, y, test_size=0.1, random_state=2018)
The ELMo residual LSTM model
batch_size = 32
Now we can initialize the ELMo embedding from tensorflow hub.
import tensorflow as tf
import tensorflow_hub as hub
from keras import backend as K
Initialize the tensorflow session.
sess = tf.Session()
K.set_session(sess)
If you run the following code for the first time, it will download the pretrained model. This might take a while.
elmo_model = hub.Module("https://tfhub.dev/google/elmo/2", trainable=True)
sess.run(tf.global_variables_initializer())
sess.run(tf.tables_initializer())
INFO:tensorflow:Initialize variable module_1/aggregation/scaling:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with aggregation/scaling
INFO:tensorflow:Initialize variable module_1/aggregation/weights:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with aggregation/weights
INFO:tensorflow:Initialize variable module_1/bilm/CNN/W_cnn_0:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/W_cnn_0
INFO:tensorflow:Initialize variable module_1/bilm/CNN/W_cnn_1:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/W_cnn_1
INFO:tensorflow:Initialize variable module_1/bilm/CNN/W_cnn_2:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/W_cnn_2
INFO:tensorflow:Initialize variable module_1/bilm/CNN/W_cnn_3:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/W_cnn_3
INFO:tensorflow:Initialize variable module_1/bilm/CNN/W_cnn_4:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/W_cnn_4
INFO:tensorflow:Initialize variable module_1/bilm/CNN/W_cnn_5:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/W_cnn_5
INFO:tensorflow:Initialize variable module_1/bilm/CNN/W_cnn_6:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/W_cnn_6
INFO:tensorflow:Initialize variable module_1/bilm/CNN/b_cnn_0:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/b_cnn_0
INFO:tensorflow:Initialize variable module_1/bilm/CNN/b_cnn_1:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/b_cnn_1
INFO:tensorflow:Initialize variable module_1/bilm/CNN/b_cnn_2:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/b_cnn_2
INFO:tensorflow:Initialize variable module_1/bilm/CNN/b_cnn_3:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/b_cnn_3
INFO:tensorflow:Initialize variable module_1/bilm/CNN/b_cnn_4:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/b_cnn_4
INFO:tensorflow:Initialize variable module_1/bilm/CNN/b_cnn_5:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/b_cnn_5
INFO:tensorflow:Initialize variable module_1/bilm/CNN/b_cnn_6:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN/b_cnn_6
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_0/W_carry:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_0/W_carry
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_0/W_transform:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_0/W_transform
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_0/b_carry:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_0/b_carry
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_0/b_transform:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_0/b_transform
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_1/W_carry:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_1/W_carry
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_1/W_transform:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_1/W_transform
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_1/b_carry:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_1/b_carry
INFO:tensorflow:Initialize variable module_1/bilm/CNN_high_1/b_transform:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_high_1/b_transform
INFO:tensorflow:Initialize variable module_1/bilm/CNN_proj/W_proj:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_proj/W_proj
INFO:tensorflow:Initialize variable module_1/bilm/CNN_proj/b_proj:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/CNN_proj/b_proj
INFO:tensorflow:Initialize variable module_1/bilm/RNN_0/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/bias:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_0/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/bias
INFO:tensorflow:Initialize variable module_1/bilm/RNN_0/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_0/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/kernel
INFO:tensorflow:Initialize variable module_1/bilm/RNN_0/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/projection/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_0/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/projection/kernel
INFO:tensorflow:Initialize variable module_1/bilm/RNN_0/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/bias:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_0/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/bias
INFO:tensorflow:Initialize variable module_1/bilm/RNN_0/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_0/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/kernel
INFO:tensorflow:Initialize variable module_1/bilm/RNN_0/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/projection/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_0/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/projection/kernel
INFO:tensorflow:Initialize variable module_1/bilm/RNN_1/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/bias:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_1/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/bias
INFO:tensorflow:Initialize variable module_1/bilm/RNN_1/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_1/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/kernel
INFO:tensorflow:Initialize variable module_1/bilm/RNN_1/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/projection/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_1/RNN/MultiRNNCell/Cell0/rnn/lstm_cell/projection/kernel
INFO:tensorflow:Initialize variable module_1/bilm/RNN_1/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/bias:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_1/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/bias
INFO:tensorflow:Initialize variable module_1/bilm/RNN_1/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_1/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/kernel
INFO:tensorflow:Initialize variable module_1/bilm/RNN_1/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/projection/kernel:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/RNN_1/RNN/MultiRNNCell/Cell1/rnn/lstm_cell/projection/kernel
INFO:tensorflow:Initialize variable module_1/bilm/char_embed:0 from checkpoint b'/tmp/tfhub_modules/9bb74bc86f9caffc8c47dd7b33ec4bb354d9602d/variables/variables' with bilm/char_embed
Now we create a function that takes a sequence of strings and returns a sequence of $1024$-dimensional vectors of the ELMo embedding. We will later use this function with the Lambda layer of keras to get the embedding sequence.
def ElmoEmbedding(x):
return elmo_model(inputs={
"tokens": tf.squeeze(tf.cast(x, tf.string)),
"sequence_len": tf.constant(batch_size*[max_len])
},
signature="tokens",
as_dict=True)["elmo"]
Now we can fit a residual LSTM network with an embedding layer.
from keras.models import Model, Input
from keras.layers.merge import add
from keras.layers import LSTM, Embedding, Dense, TimeDistributed, Dropout, Bidirectional, Lambda
input_text = Input(shape=(max_len,), dtype=tf.string)
embedding = Lambda(ElmoEmbedding, output_shape=(None, 1024))(input_text)
x = Bidirectional(LSTM(units=512, return_sequences=True,
recurrent_dropout=0.2, dropout=0.2))(embedding)
x_rnn = Bidirectional(LSTM(units=512, return_sequences=True,
recurrent_dropout=0.2, dropout=0.2))(x)
x = add([x, x_rnn]) # residual connection to the first biLSTM
out = TimeDistributed(Dense(n_tags, activation="softmax"))(x)
model = Model(input_text, out)
model.compile(optimizer="adam", loss="sparse_categorical_crossentropy", metrics=["accuracy"])
Comment: We need to make the number of samples divisible by the batch_size to make it work. Otherwise the last batch in keras will break the architecture. I haven’t found a fix for this yet. Please tell me if you have an idea.
X_tr, X_val = X_tr[:1213*batch_size], X_tr[-135*batch_size:]
y_tr, y_val = y_tr[:1213*batch_size], y_tr[-135*batch_size:]
y_tr = y_tr.reshape(y_tr.shape[0], y_tr.shape[1], 1)
y_val = y_val.reshape(y_val.shape[0], y_val.shape[1], 1)
And now we can finally fit the model. Since the computation of ELMo is pretty computational expensive, you better fit the model on a GPU.
history = model.fit(np.array(X_tr), y_tr, validation_data=(np.array(X_val), y_val),
batch_size=batch_size, epochs=5, verbose=1)
Train on 38816 samples, validate on 4320 samples
Epoch 1/5
38846/38846 [==============================] - 247s - loss: 0.1419 - acc: 0.9640 - val_loss: 0.0630 - val_acc: 0.9815
Epoch 2/5
38846/38846 [==============================] - 250s - loss: 0.0552 - acc: 0.9840 - val_loss: 0.0513 - val_acc: 0.9847
Epoch 3/5
38846/38846 [==============================] - 245s - loss: 0.0462 - acc: 0.9865 - val_loss: 0.0480 - val_acc: 0.9857
Epoch 4/5
38846/38846 [==============================] - 245s - loss: 0.0417 - acc: 0.9878 - val_loss: 0.0462 - val_acc: 0.9905
Epoch 5/5
38846/38846 [==============================] - 246s - loss: 0.0388 - acc: 0.9886 - val_loss: 0.0446 - val_acc: 0.9920
hist = pd.DataFrame(history.history)
plt.figure(figsize=(12,12))
plt.plot(hist["acc"])
plt.plot(hist["val_acc"])
plt.title("Learning curves")
plt.legend()
plt.show()
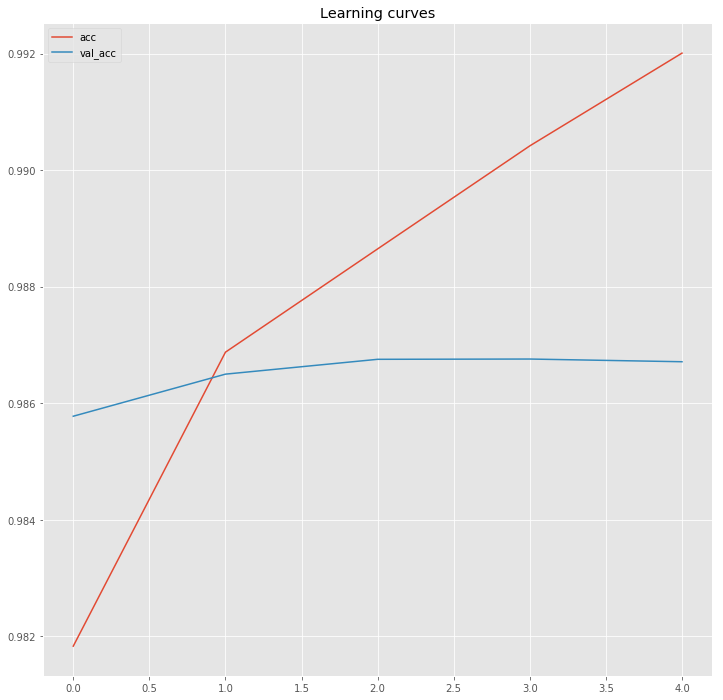
Now look at some predictions.
i = 19
p = model.predict(np.array(X_te[i:i+batch_size]))[0]
p = np.argmax(p, axis=-1)
print("{:15} {:5}: ({})".format("Word", "Pred", "True"))
print("="*30)
for w, true, pred in zip(X_te[i], y_te[i], p):
if w != "__PAD__":
print("{:15}:{:5} ({})".format(w, tags[pred], tags[true]))
Word Pred : (True)
==============================
Meanwhile :O (O)
, :O (O)
in :O (O)
Belgrade :B-geo (B-geo)
, :O (O)
Serbia :B-geo (B-geo)
's :O (O)
extreme :O (O)
nationalist :O (O)
Radical :B-geo (B-org)
Party :I-geo (I-org)
has :O (O)
filed :O (O)
a :O (O)
motion :O (O)
of :O (O)
no-confidence :O (O)
in :O (O)
the :O (O)
government :O (O)
of :O (O)
Prime :B-per (B-per)
Minister :I-per (O)
Vojislav :B-per (B-per)
Kostunica :I-per (I-per)
to :O (O)
protest :O (O)
the :O (O)
extradition :O (O)
of :O (O)
11 :O (O)
suspects :O (O)
to :O (O)
the :O (O)
court :O (O)
since :B-tim (B-tim)
October :I-tim (I-tim)
. :O (O)
This looks pretty perfect! And it did require any feature engineering! With this architecture you should be able to achieve state-of-the-art results in multiple language related sequence tagging problems. Stay tuned for more NLP posts and try some of the proposed methods yourself.
Further readings:
- Matthew E. Peters, Mark Neumann, Mohit Iyyer, Matt Gardner, Christopher Clark, Kenton Lee, Luke Zettlemoyer. “Deep contextualized word representations”
